JenI's Blog

前言

在学习第一个算法之前，先来了解一下机器学习中的两个概念，监督学习(Supervised Learning)和无监督学习(Unsupervised Learning)。

训练数据有标签向量的为监督学习。首先，我们的手上会有一批训练样本，对于每一条训练样本，我们都已知它的各个特征值和最终结果。这种情况下，我们对这些已知结果的数据进行训练，得到一个模型，之后将只包含特征的数据传入模型进行预测，得出新数据的结果。

训练数据没有标签向量的为无监督学习。无监督学习与监督学习不同的地方在于我们并不会事先准备一批数据进行训练，而是直接对数据进行建模，根据样本间的关系直接得出结果。

举个简单的例子，监督学习就好比有人事先告诉你，红色且表面光滑的是苹果，橙色且表面粗糙的是橘子，然后拿给你一个表面粗糙的橙色水果问你它是苹果还是橘子。而无监督学习就是事先什么都不跟你说，直接扔给你一堆水果，这些水果中有红色且表面光滑的，也有橙色且表面粗糙的，然后让你把这堆水果根据外观分成两堆。

k近邻算法

k 近邻算法的基本原理可以参考我的上一篇文章，这里不作赘述：

机器学习 - 常用算法的简单理解

k 近邻算法属于监督学习算法，不过它并没有训练的过程，也就是说它每次对新数据点进行分类时都会重新计算新数据点与每个样本数据点的距离，因此计算的复杂性和空间复杂度都比较高。由于要进行大量计算，所以 k 近邻算法并不太适合用在特征维度较高的分类问题上。

k 近邻算法通常使用欧式距离公式和曼哈顿距离公式来计算两点间距离。

点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的欧氏距离为：

点 p1 =（x1, y1）与点 p2 =（x2, y2）间的曼哈顿距离为：

欧式距离测量的是两点间的直线距离。而曼哈顿距离为两点所形成的对轴产生的投影的距离总和，它又被称为城市街区距离，就好比一个出租车司机从一个十字路口开到另一个十字路口的路程总和。如下图(引自维基百科)所示:

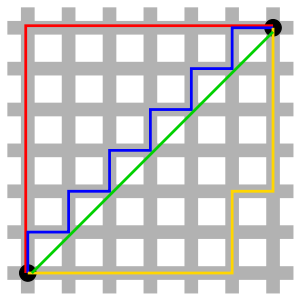
当然，可以使用的距离公式并不局限于这两种，只是这两种作为常用距离公式被广为人知。下面使用 python 实现的 k 近邻算法是基于欧式距离公式的。

k 近邻算法的 Python 实现

k 近邻算法的核心就是计算距离，所以首先编写计算两点间欧式距离的函数。

import numpy as np
import math

def euclidean(list_a,list_b):
    '''
    说明：函数接收两个列表，转换为 array 后相减，再求其平方和，最后计算出它的平方根。
    返回：浮点型数字
    '''
    array_a, array_b = np.array(list_a), np.array(list_b)
    distance = math.sqrt(sum((array_a-array_b)**2))
    return distance

有了计算距离的函数后，就可以根据计算出的距离对未知数据进行分类了。这里需要用到 operator 模块，在对邻居的种类进行排序时会用到。

import operator

def kNNClassifier(train_X, train_y, unknown_data, k):
    '''
    说明：函数接收四个参数，第一个参数为已知类别的数据集(列表：[[],[],[]...])，第二个参数是已知类别数据集的标签向量，第三个参数为待分类的数据点(列表：[...])，第四个参数为邻居数量。
    返回：字符串
    '''
    # 判断 k 值是否过大，如果 k 值比原始数据集还大，则直接退出函数。
    if k > len(train_X):
        return '[-]Error: The k value is too large!'
    distances = []
    tmp = {}
    # 计算待分类的数据点与已知类别数据集中各点的距离。
    for i in train_X:
        distance = euclidean(i, unknown_data)
        distances.append(distance)
    # argsort 函数返回数组值从小到大的索引。
    index = np.array(distances).argsort()
    # 统计距离待分类数据点最近 k 个点的类别数量。
    for i in range(k):
        tmp[train_y[index[i]]] = tmp.get(train_y[index[i]], 0) + 1
    nerghbors_count = tmp.items()
    # 以数量为依据进行降序排序。
    nerghbors_count.sort(key=operator.itemgetter(1), reverse=True)
    # 最终返回 k 个邻居中最多的类别。
    return nerghbors_count[0][0]

现在我们编写了 k 近邻算法的分类器，可以试着使用这个分类器对未知数据进行分类了。这里我使用了十分流行的鸢尾花数据集，这份数据集共有 150 条数据，每一条数据包含 4 个特征值和 1 个目标变量。下图为每种花卉的各三条数据。

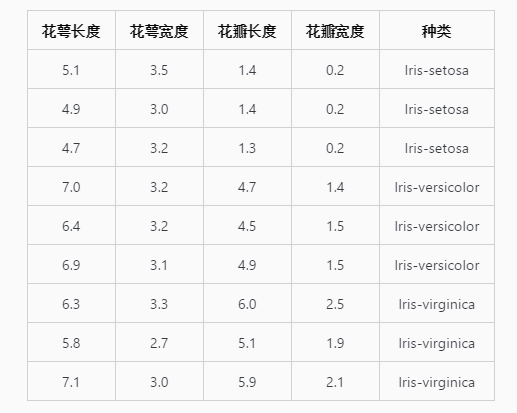
我将鸢尾花数据集整理成了文本格式，有需要的同学可以直接点击下边的链接下载

鸢尾花数据集

编写函数将鸢尾花文本数据集处理为我们分类器可用的格式：

def load_iris():
    '''
    说明：函数读取 iris 文件内容，处理为可用于分类器的格式。
    返回：列表，列表
    '''
    data, label = [], []
    with open('iris','r') as f:
        for i in f.readlines():
            i = i.strip().split('\t')
            data.append([float(x) for x in i[:-1]])
            label.append(i[-1])
    return data, label

现在尝试使用分类器对未知数据进行分类，假设我们有一个花萼长度为 5.8、花萼宽度为 2.7、花瓣长度为 4.1、花瓣宽度为 1.0 的花需要判断种类，我们将这个花的数据放入分类器进行判断，结果如下：

train_X, train_y = load_iris()
unknown_data = [5.8, 2.7, 4.1, 1.0]
category = kNNClassifier(train_X, train_y, unknown_data, 3)
print category

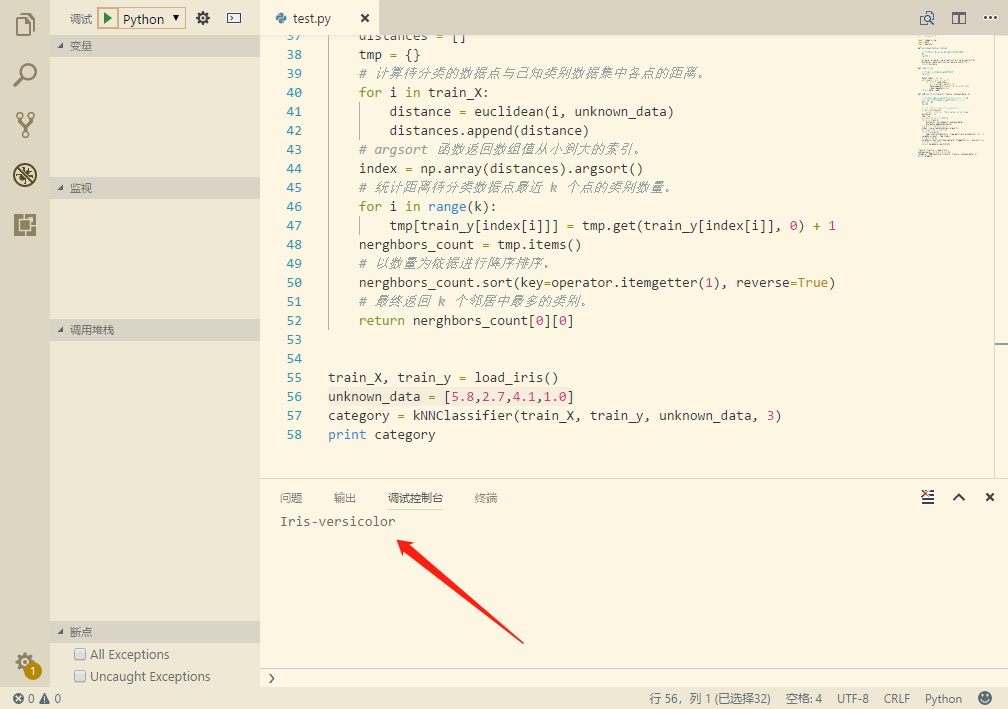
可以看到分类器判断这朵花的种类为 Iris-versicolor。

kNN 算法在 sklearn 中的使用

下图为 sklearn 库中 kNN 算法的相关函数，包括了几种常用邻居搜索算法、基于 k 近邻的回归器、核密度估计、质心分类器等多个方面：

其中对于几种常用邻居搜索算法，sklearn.neighbors 为其提供了统一的接口。通过 NearestNeighbors 中的 algorithm 关键字可以十分方便的选择使用 BallTree、KDTree 还是 Brute Force 暴力算法(BF)，这些算法各有优势，但不在本文的介绍范围内。这里由于只是想对数据进行简单分类，所以只介绍 KNeighborsClassifier() 方法，具体使用方法如下：

# 从 sklearn 的数据集中导入 load_iris 方法，该方法用于加载鸢尾花数据集
from sklearn.datasets import load_iris
# 导入 k 近邻分类器
from sklearn.neighbors import KNeighborsClassifier

unknown_data = [5.8, 2.7, 4.1, 1.0]
# 加载数据集
iris = load_iris()
# 声明一个分类器实例
knn = KNeighborsClassifier()
# fit 方法是 sklearn 库在最初设计时提供的统一 API，分类、回归、聚类、维数约减、特征抽取、数据预处理这六大板块都包含 fit 方法
knn.fit(iris.data, iris.target)
# predict 方法只有分类、回归、聚类三个板块有。这里用作对未知数据进行结果预判
predict = knn.predict([unknown_data])
print iris.target_names[predict]

KNeighborsClassifier() 函数可接受的参数有很多个：

n_neighbors : int, optional (default = 5)

    weights : str or callable, optional (default = 'uniform')

    algorithm : {'auto', 'ball_tree', 'kd_tree', 'brute'}, optional

    leaf_size : int, optional (default = 30)

    metric : string or DistanceMetric object (default = 'minkowski')

    p : integer, optional (default = 2)

    metric_params : dict, optional (default = None)

    n_jobs : int, optional (default = 1)

n_neighbors 是指要搜素的最近邻数量，默认为 5；weights 是对邻居权重的配置；algorithm 是决定使用哪种近邻算法的参数，默认是自动，即分类器会从这些算法中试图找到对训练集最合适的算法；leaf_size 是叶片大小，只有在使用 BallTree 和 KDTree 时这个参数才有意义，默认 30；metric 参数的默认值是 minkowski，即闵式距离。实际上闵式距离并不是一种距离，而是一组距离的定义，可以把他当作是距离公式的选择器，它与下一个参数 p 相关，当 p=1 时，使用曼哈顿距离，p=2 时，使用标准欧氏距离，当 p>2 时，就是切比雪夫距离；还有一个 n_jobs 参数，这个参数表示使用多少个 CPU 核并行搜索，默认为 1。这里我们全部使用默认值，运行结果和我们自己编写的分类器结果一致：

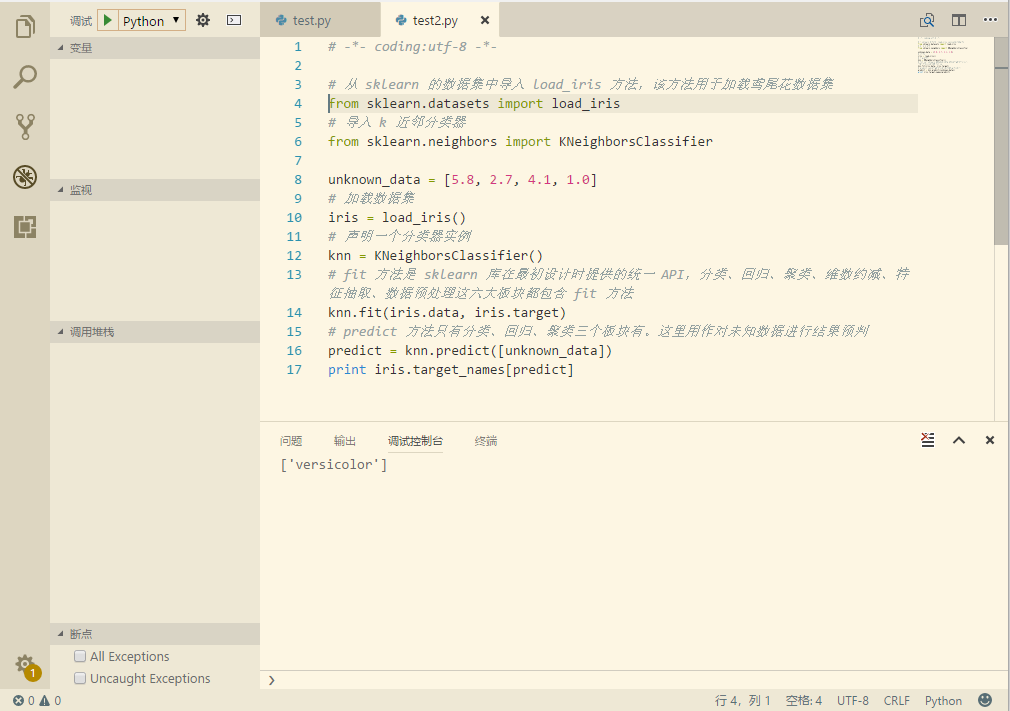
参考

http://scikit-learn.org/dev/modules/classes.html#module-sklearn.neighbors http://scikit-learn.org/dev/modules/neighbors.html#neighbors

作者: JenI 转载请注明出处，谢谢

机器学习 - k近邻算法

Comments !