前言
机器学习,英文名叫Machine_Learning,是实现人工智能的一种方法,属于人工智能的一个分支。机器学习涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等多门学科,是一个多领域交叉的综合学科。它的原理主要是设计和分析一些让计算机可以自己“学习”的算法。这些算法从已知数据中分析出规律,再利用这些规律对新的数据进行预测。从而完成分类、决策、预测等多种问题。
最近由于人工智能、深度学习、自动驾驶这些话题热度十分的高,再加上公司有相关业务,所以我也开始着手学习机器学习相关的知识,但是说实话,学习这些内容对于我这个学渣来说确实极具挑战性,不过好在目前国内外有许多优秀的书籍和文章对机器学习相关知识做了深入浅出的讲解,对我这种初学者起了很大的帮助。
机器学习发展至今,已经出现了很多成熟的算法,其中最为常用的有以下几种:
- k近邻(k-Nearest Neighbour, kNN)
- 决策树(Decision Tree)
- 随机森林(Random forest)
- 支持向量机(Support Vector Machine, SVM)
- 逻辑(logistic)回归(logistic regressive)
- K均值(K-means)
- 朴素贝叶斯(Naive Bayesian Model)
- 神经网络(Neural network algorithm)
我会对上述的几个算法原理做大概的介绍,在之后的文章中会针对每一种算法做详细解释,并介绍该算法在 scikit-learn 库中的使用方法。如果有精力,我也会使用 Python 语言自己实现该算法,以便自己和阅读这系列文章的人加深对该算法的理解。
k近邻
k 近邻算法的思想非常简单,也很容易理解,就是当为一个新的数据点划分种类时,会首先找到距离该数据点最近的 k 个点,看看他们分别属于什么类,哪个类数量多就认为这个新的数据点是哪个类。举个例子:

在上图中,我们使用耳朵(现实中耳朵并不是一个适合区分猫和狗的特征,这里只是举个例子)和叫声来区分猫和狗,黄色圆点代表猫类,蓝色圆点代表狗类。现在我们有一个未知种类的动物(紫色圆点)需要判断种类。假设 k 为 3,也就是选取距离这个紫色圆点最近的 3 个点,这三个点中,两个属于猫类,一个属于狗类,所以我们说这个未知种类的动物属于猫类。
决策树
决策树相当于是数个if-else 语句构成的嵌套结构的判断流程,它根据数据集中的特征进行分类,在每个节点进行判断,满足为一类,不满足为另一类,也就是执行了一次 if-else,多次之后最终形成一个树形。使用《Machine Learning in Action》一书中的例子来做解释:
下面有一组海洋生物的数据
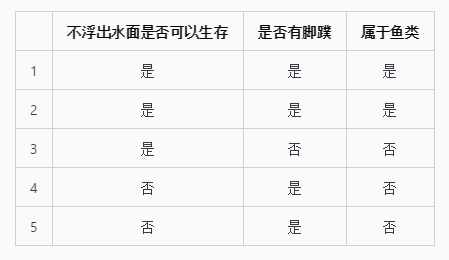
数据表中的两个判断条件(不浮出水面是否可以生存、是否有脚蹼)被称为数据的特征,最后的一列(是否为鱼类)是数据的标签向量。根据数据表可以得出以下树形图:
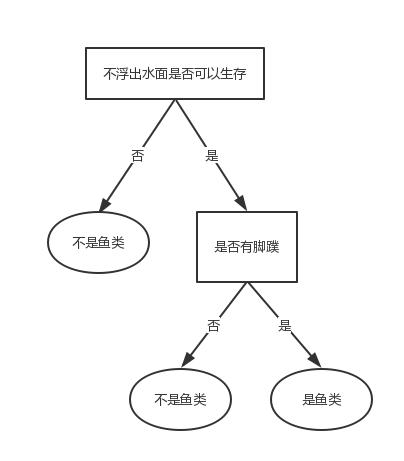
当有新的海洋生物需要被分类时,根据树形图,首先判断它在不浮出水面的情况下是否可以生存,如果不可以,说明不是鱼类,如果可以,则判断它是否有脚蹼,有的话属于鱼类,没有就不属于鱼类。这就是一个最简单的决策树。
随机森林
随机森林可以说是决策树的加强版。决策树算法相当于根据所有原始数据中的特征和标签向量建立起一颗大树,而随机森林是首先将原始数据随机分成多个子数据集,再为每个子数据集单独建立起一个决策树,如下图所示:
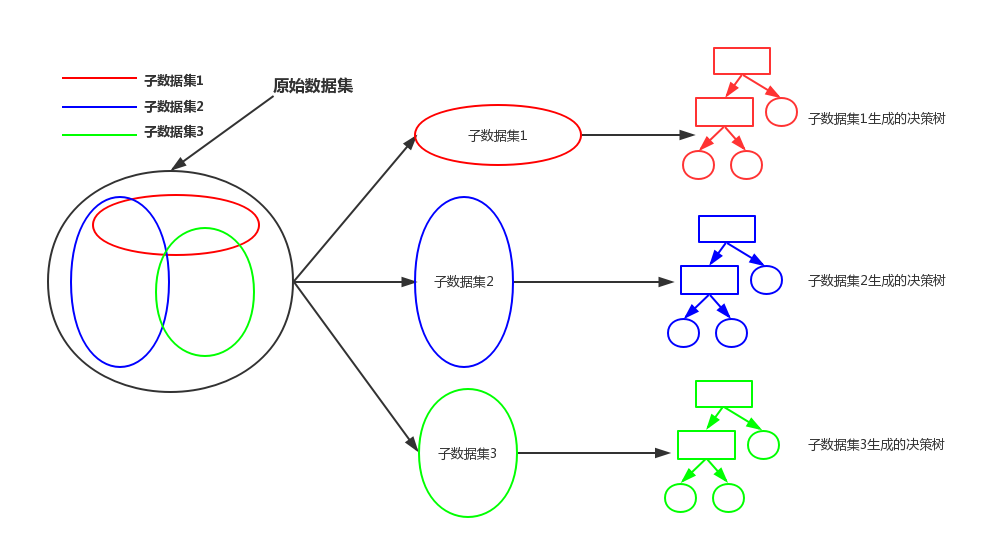
当有新的数据输入时,会将这个数据分别放到这些子数据集建立的决策树内进行分类,分出的类别依然满足 “少数服从多数” 的原则,即决策树分出的哪个类别多,就认为新的数据属于哪个类别。
支持向量机
支持向量机相对比较复杂,既可以用于分类问题,也可以用于回归问题。我这里依然使用简单的分类问题来说明支持向量机。首先考虑一维的情况,我们使用直径来对篮球和乒乓球分类,假设以 14cm 作为判断依据,小于 14cm 的为乒乓球,大于 14cm 的为篮球,从而得出下面的数轴:
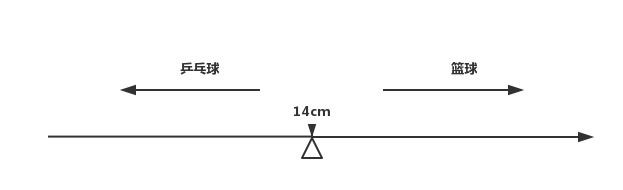
我们有新的球要分类时,将这个球类的直径大小放在这条数轴上进行判断,位置在左侧为乒乓球,在右侧为篮球。
然后是二维的情况,假设我们使用重量和材质两个特征来辨别实心球和铅球,把已知的数据放到一个平面直角坐标系中,根据重量和材质两个特征,不同类别的数据会聚在一起,这时,我们找到一条线,将这两个类别划分开来,之后再有新的数据,把它根据重量和材质两个特征丢到坐标系中,在直线哪侧就说明它属于哪个类,至于如何找到这条分类线,我会在之后的文章中详细说明。下面是示意图:
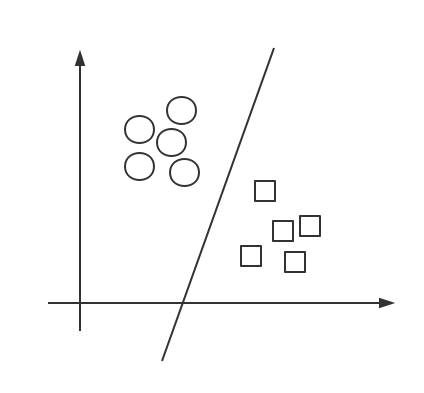
三维、四维到 N 维就由找点找线的问题变为了找平面找超平面的问题。除了进行线性分类,支持向量机可以使用核函数,核函数用来处理非线性的问题,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。举个例子:假设我们在划分种类时得到的分类函数并不是像上面那种直线函数,而是一个圆函数,x^2 + y^2 = 4,这时我们另 a = x^2,b = y^2,从而得到 a + b = 4 ,此时这个圆函数分类问题就变成了直线分类问题了。
逻辑回归
线性回归常用于分析两个变量 X 和 Y 之间的关系,比如铁球的大小与铁球的重量之间的关系,这种关系可以使用特征值和它对应的概率相乘得到的结果来表示。逻辑回归可以看作是在线性回归的结果上加上了一个回归函数,对函数的值域进行了最大和最小值的限制。逻辑回归虽然叫做回归,但是更多情况都将它用作二分类问题。
先来说说线性回归。一个自变量一个因变量且可以用一条直线描述他们之间的关系的回归称为一元线性回归,即 y = ax + b,两个以上自变量或两个以上因变量且他们之间是线性关系的回归称为多元线性回归。 我用一元线性回归来举例(图片引自维基百科):
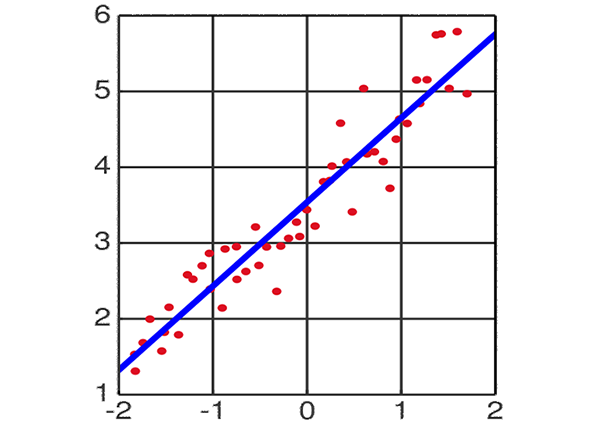
上面图片中有很多的数据点,我们找到一条直线,使这些数据点到这条直线的距离之和最小,这条直线就是用来描述特征间关系的回归直线。但是这样的直线很容易受到“噪声”影响,如下图所示:
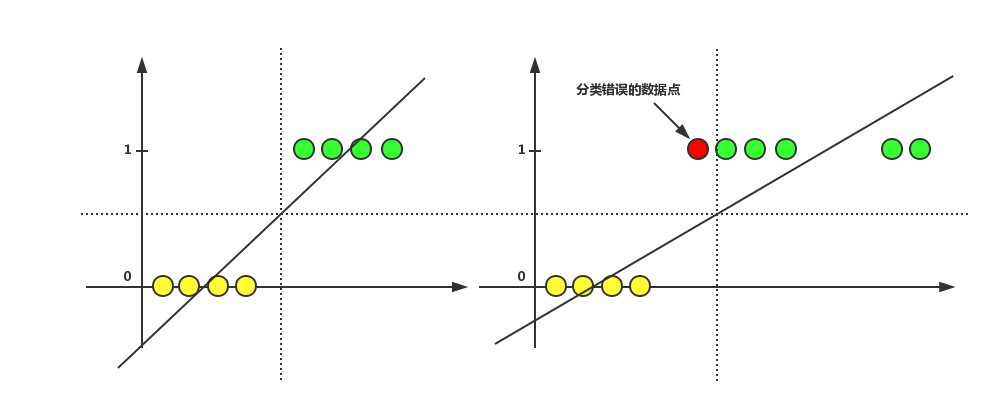
假设图中直线方程使用 y = ax + b 来表示,黄色数据点的 y 为 0,绿色数据点的 y 为 1,通过这两种数据点拟合出一条回归直线。左侧为无噪点的情况,右侧为有噪点的情况(右侧图中比左侧多出的数据点为噪点),左右对比可以发现,当存在噪点时,回归直线受噪点影响,将一个值本来为 1 的数据点错误的归为了 0 类,此时的阈值 0.5 就不再适合对右侧图片中的情况做分类了。而且现实中的分类情况往往比上图描述的复杂得多,很难通过线性回归和阈值来进行准确的分类。于是,逻辑回归就出现了。
逻辑回归使用 sigmoid 函数将数据的值域控制在 [0,1] 之间。sigmoid 函数又叫 S 函数,这个函数的作用是把任何连续的值映射到 [0,1] 这个区间内,数越大越趋近于 1 ,数越小越趋近于 0。像下面这样(图片引自维基百科):
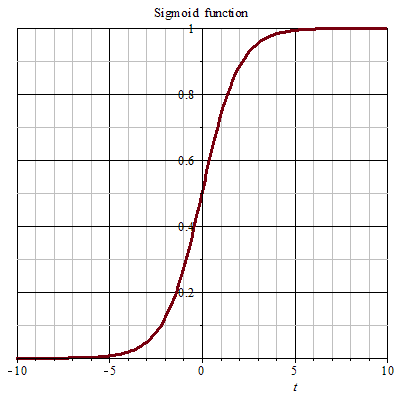
此时的 y 值可以看作是数据点为 1 的概率,大于 0.5 就认为该数据点属于 1 类,小于 0.5 则属于 0 类。
K均值
K 均值算法是聚类算法中相对简单的一种,用于将数据点聚合成 k 类。这个 k 是个常量,需要我们手动指定,也就是说,我们想要将数据点分为几类,就需要将 k 值设定为几。下面的图中,我们设 k 的值为 2:
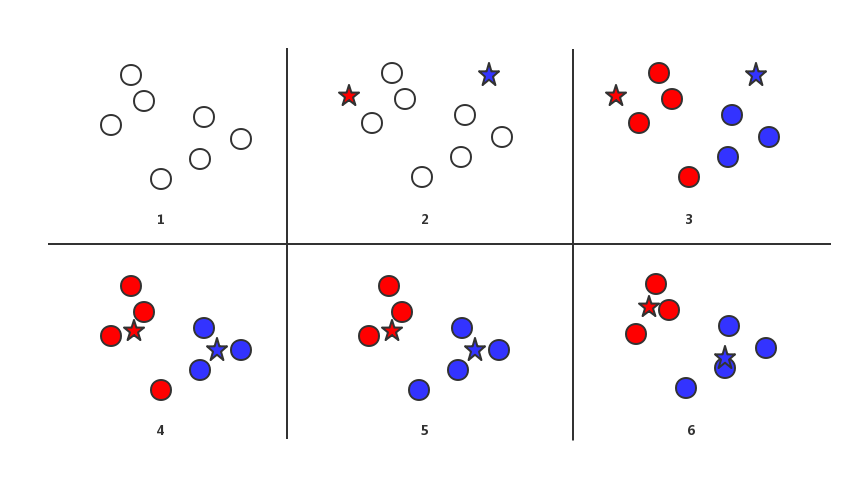
图 1 中显示的无颜色圆点表示原始数据点,图 2 为 k 均值算法的第一步,我们随机选择了两个点作为初始点,也就是红蓝两色五角星标识的位置。第二步,我们依次取出一个圆点,计算出它与两个五角星的距离,哪个距离近,就将这个圆点标为哪种颜色,直到所有圆点都被上色,此时如图 3 所示。第三步,我们不看这两个五角星,只看两种颜色的圆点,求出他们各自的质心,将各自种类的五角星移动到这个位置。之后多次重复第二步和第三步,直至质心的位置不在变化或变化很小为止。此时,原始数据点就被分为了 2 类。
朴素贝叶斯
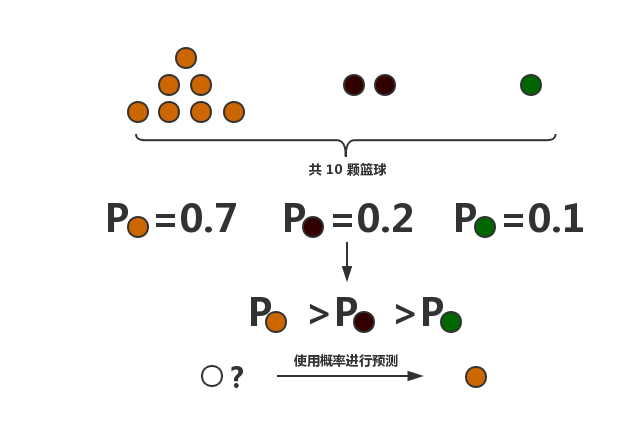
朴素贝叶斯是一种通过概率对数据进行分类的算法,使用了概率论中的贝叶斯原理。之所以叫朴素贝叶斯,是因为我们假设数据的特征之间是没有关系的,也就是说每一个特征发生的概率对最终结果的影响都是独立的。因为多特征的情况描述起来比较繁琐,我留到之后的文章中说明,这里还是使用最简单的单特征情况举例:假设我们有 10 个篮球,其中7个是棕色,2 个黑色,1 个青色,此时篮球为棕色的概率是 0.7,为黑色的概率是 0.2,为青色的概率是 0.1。P(棕色)>P(黑色)>P(青色),再有新的篮球需要判断颜色时,由于棕色概率最高,朴素贝叶斯分类器就会认为这颗篮球是棕色的。
神经网络
神经网络通过模仿生物神经网络的工作原理来做一些复杂的分类运算,因此而得名。神经网络一般会涉及两种传播方式,正向传播和反向传播。
首先了解一下神经元。神经元其实可以理解为一个小型的计算器,它接受上一层传入的数据,计算线性加权和后传入激活函数,如下图

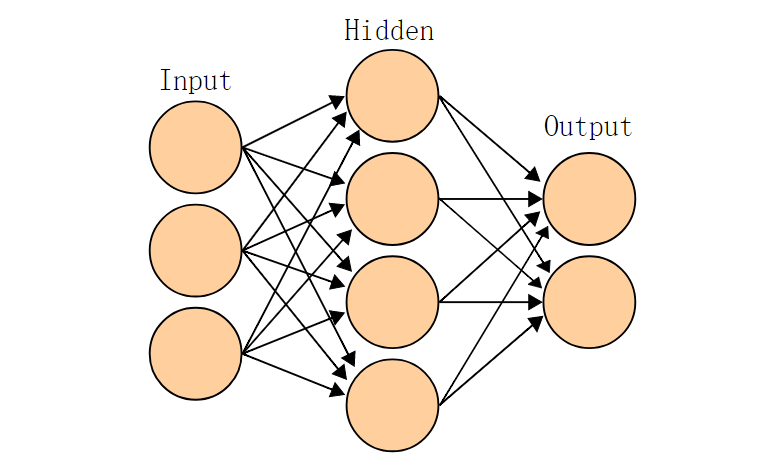
线性加权和是指将每个输入的值和其对应的权重相乘后再求和,激活函数是我们自己指定的,可以使用 0-1 阶跃、sigmoid 等非线性函数。这就是神经网络里的一个神经元的工作流程。其中权重是一个很重要的东西,因为训练一个神经网络时,输入输出和激活函数都是给定的,唯一可变的就是这个权重,所以训练神经网络的过程就是不断调整权重使其达到最佳的过程,这样整个神经网络的预测效果才会最好。神经元的输出是下一层神经元的输入,每层神经元与下一层神经元连接,最终构成了神经网络,一个神经网路通常包含输入层,隐藏层,以及输出层,如下图所示(图片引自维基百科):
作者: JenI 转载请注明出处,谢谢
Comments !